在unity中实现真实感布料

总的参数与大纲

这次做了一个基本不会用上的东西，毕竟为了布料花上这么大的消耗不太划算，除非是暖暖一类的换装游戏。回到正题，之前做毕设的时候就在研究这个模型，但是当时不太行没有发现问题。参考的文献是《A Practical Microcylinder Appearance Model for Cloth Rendering》¹，还有一篇博客。这篇博客相当详细的说明了他参照文献的实现过程，不过是在houdini里面模拟的。英文好日语好的可以去看看。

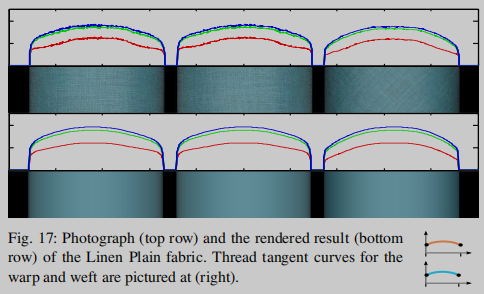
文献使用光追渲染的效果如下。

文献渲染的结果

可以发现，这个基于微圆柱体的模型的特点就是，经纬线的参数可以不同，使用不同的参数可以组合表现的范围很广，平织的、丝绸、生丝、天鹅绒都能模拟。

参数主要有这几个，对于经线纬线各有一套，也就是一共两套：

参数	意义
Color	颜色
Alpha	比例
IOR	折射率
Glossiness	光泽度
Isotropy	各向同性
TangentOffset	织线弯曲的斜率，是一个数组

在unity的材质编辑器里面看起来是这样：

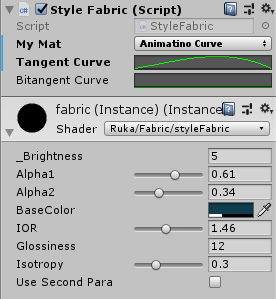
unity的材质编辑器

需要注意的是TangentOffset这个参数我用的是Unity自带的AnimationCurve来实现，采集每个点的斜率。另外启用了Use Second Para选项才会出现第二套参数。Brightness是整体的亮度调节。

计算大纲

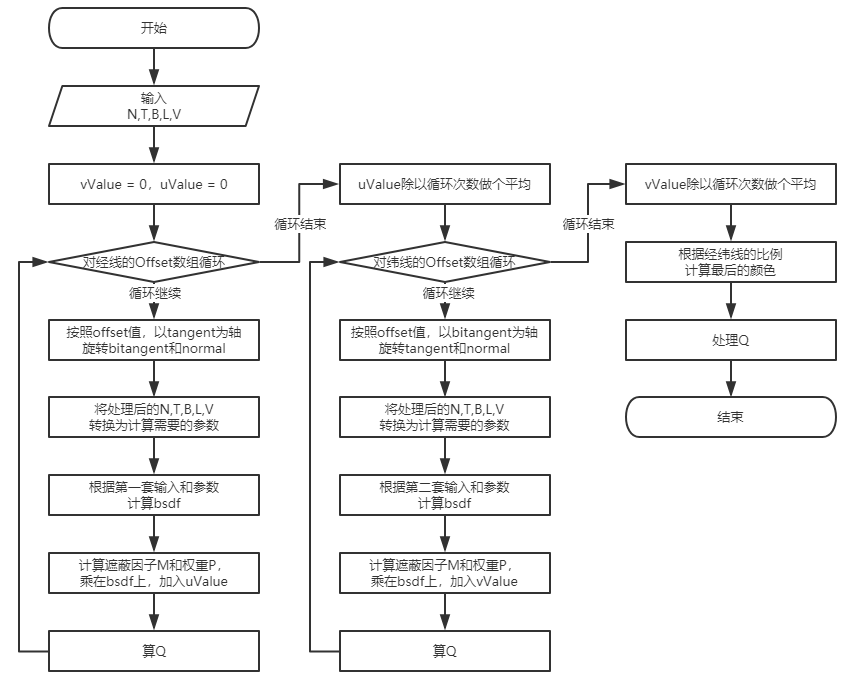
以上是整体完成之后给出的大纲，下面说一下每个部分的细节。

Tangent Curve

这个东西可以理解为织线弯曲的情况，这种弯曲是从侧面观察的。

切曲线

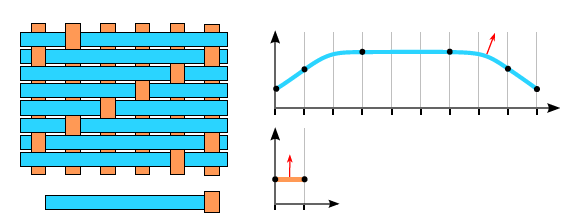
蓝色代表的线说明两头被压下去，中间鼓起来一些。橙色的线两头被压得太紧，没有这种弧度。每个黑点都是一处采样点，每有一个采样点就根据其该点在曲线上的斜率做一次流程图里的循环。

这种表达方式虽说感觉很玄幻，但是参照一下文献里面的示例大概可以理解一点。比如平织的亚麻布，经线和纬线都是均匀放置的，所以两个tangentCurve相同，都是中间微微凸起。

亚麻切曲线

一个极端的例子是天鹅绒，他的tangentCurve中间有斜率不连续的点而且翘起，这应该是模拟那种毛绒绒的感觉。

天鹅绒切曲线

这一块的实现借助了Unity的AnimationCurve，在Update函数中定义其用法：

Keyframe[] keyPointsU = tangentCurve.keys;
Keyframe[] keyPointsV = bitangentCurve.keys;
float[] arrayU = new float[arrayLen];
float[] arrayV = new float[arrayLen];
for (int i = 0; i < keyPointsU.Length && i < arrayLen; i++)
{
    // Debug.Log(i + " " + keyPointsU[i].inTangent);
    arrayU[i] = Mathf.Atan(keyPointsU[i].inTangent);
}
mAC.SetFloatArray("tangent_offsets_u", arrayU);
mAC.SetInt("numU", keyPointsU.Length);
for (int i = 0; i < keyPointsV.Length && i < arrayLen; i++)
{
    // Debug.Log(i + " " + keyPointsV[i].inTangent);
    arrayV[i] = Mathf.Atan(keyPointsV[i].inTangent);
}
mAC.SetFloatArray("tangent_offsets_v", arrayV);
mAC.SetInt("numV", keyPointsV.Length);
rd.sharedMaterial = mAC;

这样我们就能把需要的数据从脚本处理传到shader中。

根据当前的Offset旋转法线和切线/负切线

这一块没啥好说的，需要注意的是unity shader中没有我们需要的rotate函数，自己定义一个就好。

half3 rotate(half3 v, half angle, half3 axis)
{
    half cosa, sina;
    sincos(angle, sina, cosa);
    
    half oneMinusA = 1.0 - cosa;
    float3x3 rotateM = {
        cosa + oneMinusA * axis.x * axis.x,
        oneMinusA * axis.x * axis.y - sina * axis.z,
        oneMinusA * axis.x * axis.z + sina * axis.y,
        oneMinusA * axis.x * axis.y + sina * axis.z,
        cosa + oneMinusA * axis.y * axis.y,
        oneMinusA * axis.y * axis.z - sina * axis.x,
        oneMinusA * axis.x * axis.z - sina * axis.y,
        oneMinusA * axis.y * axis.z + sina * axis.x,
        cosa + oneMinusA * axis.z * axis.z
    };
    return mul(rotateM, v);
}

如果我们需要以负切线v为轴，将法线normal旋转tangent_offset度，就可以写为：

half3 n = rotate(normal, tangent_offsets_u[i], v); //i是当前的循环值

处理参数

通过前面的一系列处理，目前的参数有：旋转后的法线、切线、负切线以及shader里面自行获取的光线和视线方向。为了匹配原文献中的数学公式，这里将参数转化一下：

struct PARA
{
    half thetaD;
    half thetaH;
    half cosThetaI;
    half cosThetaO;
    half phiD;
    half cosPhiI;
    half cosPhiO;
    half psiD;
    half cosPsiI;
    half cosPsiO;
};

$\theta$、$\phi$、$\psi$的定义见图：

坐标系

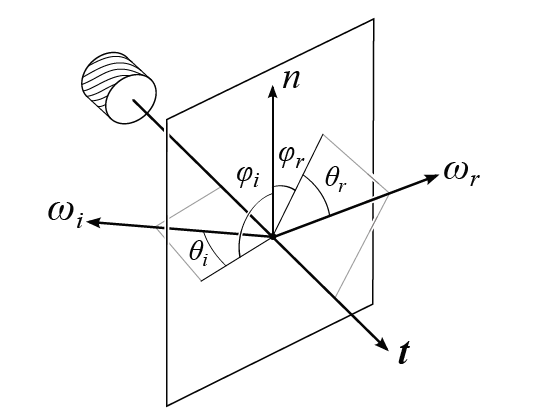
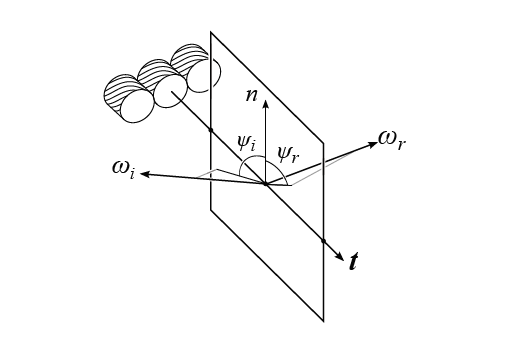
void parameterize(half3 T, half3 B, half3 N, half3 L, half3 V, inout PARA p)
{
    half LoT = dot(L, T);
    half VoT = dot(V, T);
    
    half thetaI = asin(LoT);
    half thetaO = asin(VoT);
    p.cosThetaI = cos(thetaI);
    p.cosThetaO = cos(thetaO);
    p.thetaD = (thetaI - thetaO) * 0.5;
    p.thetaH = (thetaI + thetaO) * 0.5;
    
    half3 L_NP = normalize(L - T * LoT);
    half3 V_NP = normalize(V - T * VoT);
    half phiI = acos(dot(L_NP, N));
    half phiO = acos(dot(V_NP, N));
    p.phiD = phiI - phiO;
    p.cosPhiI = dot(N, L_NP);
    p.cosPhiO = dot(N, V_NP);
    
    half3 L_TN = normalize(L - B * dot(L, B));
    half3 V_TN = normalize(V - B * dot(V, B));
    half psiI = acos(dot(L_TN, N));
    half psiO = acos(dot(V_TN, N));
    p.psiD = psiI - psiO;
    p.cosPsiI = dot(N, L_TN);
    p.cosPsiO = dot(N, V_TN);
}
    

计算bsdf

原文献的bsdf分为了三个部分：

微圆柱体的菲涅尔
反射
散射

其中反射和散射的比例由菲涅尔决定。菲涅尔项用了《Microfacet Models for Refraction through Rough Surfaces》²中的实现：

inline half microcylinder_fresnel_dielectrics(half cosTheta, half ior)
{
    half c = cosTheta;
    // half g = sqrt(sqr(eta_t) / sqr(eta_i) - 1.0 + sqr(c));
    half g = sqrt(sqr(ior) - 1.0 + sqr(c));
    
    half a = 0.5 * sqr(g - c) / sqr(g + c);
    half b = 1.0 + sqr(c * (g + c) - 1.0) / sqr(c * (g - c) + 1.0);
    return a * b;
}

half Fr_cosTheta = cos(p.thetaD) * cos(p.phiD * 0.5);
half Fr = microcylinder_fresnel_dielectrics(Fr_cosTheta, input.ior);
half F = (1 - Fr) * (1 - Fr);

反射rs与散射rv用到了normalized_gaussian：

inline half normalized_gaussian(half beta, half theta)
{
    half x = 2 * beta * beta;
    return exp(-theta * theta / x) / sqrt(UNITY_PI * x);
}

half rs = Fr * cos(p.phiD * 0.5) * normalized_gaussian(input.gloss, p.thetaH);
half rv = F * ((1 - input.isotropy) * normalized_gaussian(input.gloss * 2, p.thetaH) + input.isotropy) / (p.cosThetaI + p.cosThetaO);

输出需要除以thetaD的cos值的平方：

half3 res = rv * input.color + half3(rs, rs, rs);
res /= sqr(cos(p.thetaD));

计算遮蔽阴影M和reweighting P

这两项的计算非常相似，所以放到一个函数里，区别是参数不同，M对应$\phi$，P对应$\psi$：

inline half microcylinder_MP(half cosI, half cosO, half d)
{
    half m_i = saturate(cosI);
    half m_o = saturate(cosO);
    half corrated = min(m_i, m_o);
    half uncorrated = m_i * m_o;
    
    half u = exp(-4.082 * d * d);
    return lerp(uncorrated, corrated, u);
}

half mValue = microcylinder_MP(p.cosPhiI, p.cosPhiO, p.phiD);
half pValue = microcylinder_MP(p.cosPsiI, p.cosPsiO, p.psiD);

最后

我尝试了分别用vert和frag计算，的确frag的效果好上很多，但相机不可以开msaa，否则会出现很多破面（还不知道为什么）。

这是文献里面生丝的渲染效果：

坐标系

Sadeghi I, Bisker O, De Deken J, et al. A practical microcylinder appearance model for cloth rendering[J]. ACM Transactions on Graphics (TOG), 2013, 32(2): 1-12. ↩
Walter B, Marschner S R, Li H, et al. Microfacet Models for Refraction through Rough Surfaces[J]. Rendering techniques, 2007, 2007: 18th. ↩

上篇在unity中实现基于PBR的丝绸材质

下篇Unity的地形开发管线